La división en matemáticas es el proceso de separar un número en partes iguales y averiguar cuántas de ellas se pueden formar. Por ejemplo, dividir 15 entre 3 significa separar 15 en 3 grupos iguales de 5. Siga leyendo para aprender qué es una división, cuáles son sus partes y sus criterios de divisibilidad, y cómo se realizan.

¿Qué es una división?
La división es una operación aritmética primaria en la que los números se combinan y dividen de tal manera que forman un nuevo número. Esto significa que dividiremos un número con otro y se formará un tercer número completamente nuevo. La división es un método para agrupar objetos por igual en grupos, como organizar a los estudiantes en filas durante un desfile.
Entonces, ¿qué es la división? En resumen es el proceso de resta repetitiva que se denota mediante un símbolo matemático que consiste en una línea horizontal corta con un punto por encima y por debajo de la línea. Para realizar operaciones que nos obligan a dividir, utilizamos ciertos símbolos como: ÷ y /. Por ejemplo, 4 ÷ 2 = 2 y 4/2 = 2
Casos especiales
A continuación se presentan tres casos especiales de división:
- Cualquier número que se divide por 1 (el cociente es igual al dividendo), da la misma respuesta que el dividendo. Por ejemplo: 10 ÷ 1 = 10
- Un número no se puede dividir por 0 y, por lo tanto, el resultado no está definido. Ejemplo: 60 ÷ 0 = indefinido (pero 0 ÷ 60 = 0)
- Cuando el dividendo es igual al divisor, lo que significa los mismos números pero no 0, entonces la respuesta es siempre 1. Por ejemplo: 41 ÷ 41 = 1
Cuál es la fórmula general para la división
La fórmula general para la división requerirá que tengamos el dividendo, el cociente, el divisor y el resto. El significado de cada uno de estos términos se podrá entender mejor con la información que encontrará debajo en el artículo. Lo mismo si está buscando aprender a dividir, a continuación le explicaremos paso a paso cómo hacerlo.
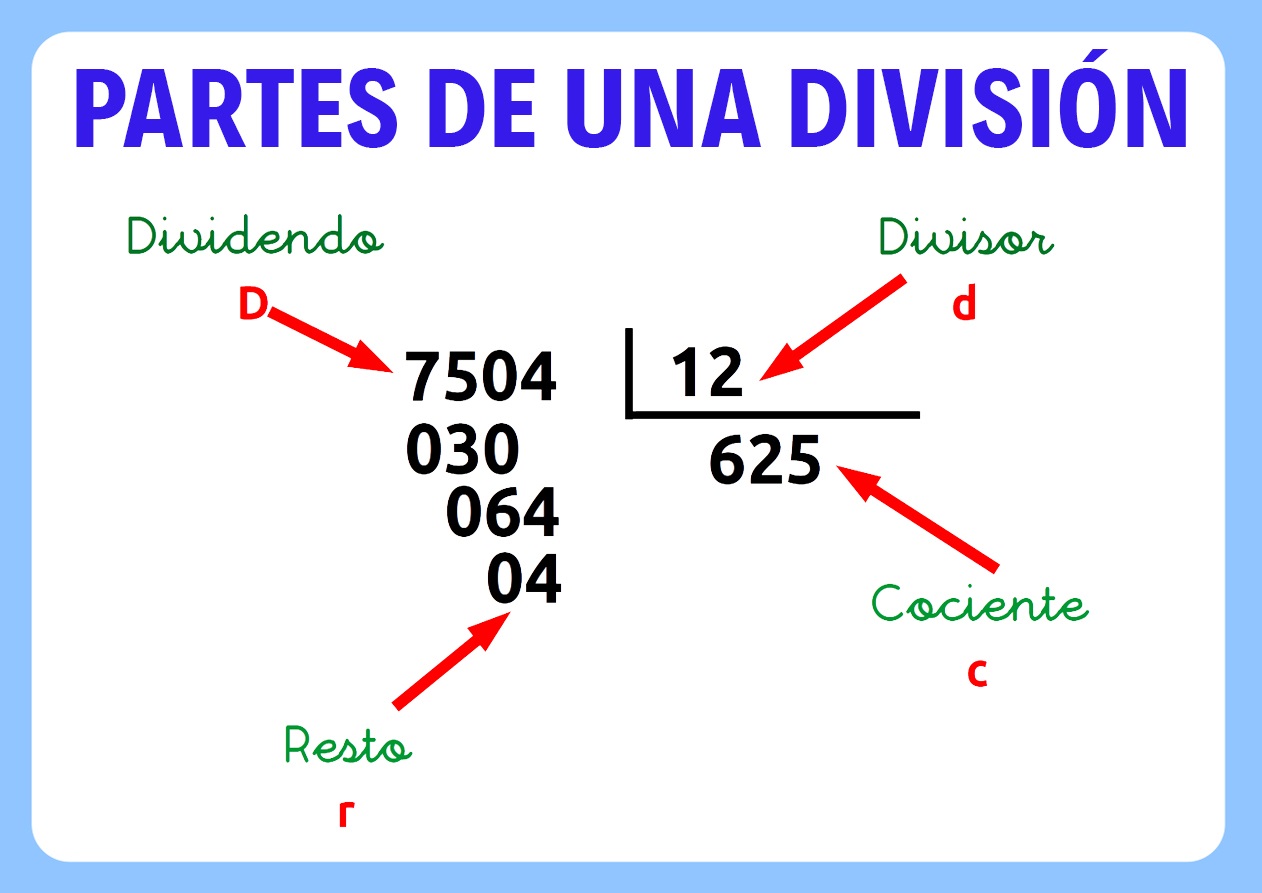
La fórmula general de la división es: Dividendo = (Divisor × Cociente) + Resto
Verificación del resultado de la división
Podemos verificar fácilmente si nuestra respuesta es correcta o incorrecta. Como la división es el reverso de la multiplicación, averiguaremos cómo podemos verificar nuestra respuesta usando esta información. Por ejemplo, 6 ÷ 2 = 3, resto = 0. En otras palabras, 6 = 2 × 3 + 0. Esto se puede expresar como Dividendo = (Divisor × Cociente) + Resto.
Vamos a utilizar el siguiente ejemplo para hacer la verificación:
- Dividendo = 105
- Divisor = 8
- Cociente = 13
- Resto = 1
Sustituyendo los valores en la fórmula, obtenemos 105 = (8 × 13) + 1 = 104 + 1 = 105. Por tanto, nuestra respuesta es correcta.
Método de división larga
El método de división larga es el método más común utilizado para resolver problemas de división. En este proceso, el divisor se escribe dentro del símbolo de visión en el margen derecho, mientras que el dividendo se coloca a la izquierda fuera del mismo. El cociente se escribe debajo del divisor, fuera del paréntesis. El cociente en matemáticas se puede definir como el resultado de la división entre un número y cualquier divisor. Es el número de veces que el divisor está contenido en el dividendo sin que el resto sea negativo.
- Paso 1: tome el primer dígito del dividendo, siempre y cuando este dígito sea mayor o igual que el divisor.
- Paso 2: Luego divídelo por el divisor y escriba la respuesta debajo del paréntesis del divisor.
- Paso 3: Haga la resta y escriba debajo el resultado.
- Paso 4: nuevamente, repita el mismo proceso.
Entendamos el proceso de la división con la ayuda de un ejemplo. Intentemos realizar la siguiente división: 435 ÷ 4.
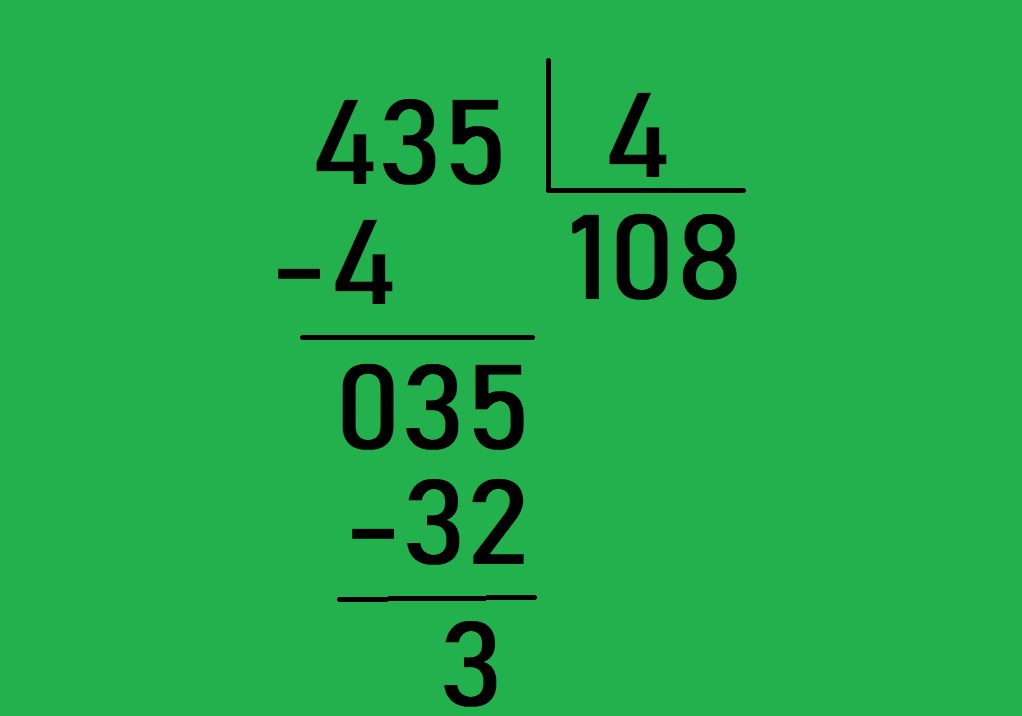
- Aquí, el primer dígito es 4 y es igual al divisor. Entonces, 4 ÷ 4 = 1; 1 va escrito en la zona del cociente. El resultado 4 × 1 = 4 se resta del dígito y se escribe 0 debajo.
- A continuación, se toma el segundo dígito o el dígito en el lugar de la decena al lado del 0. Dado que 03 es menor que 4, no podemos dividir este número. Por lo tanto, escribimos un 0 en la parte inferior y colocamos el dígito en el lugar de la unidad al lado de 3.
- Ahora, tenemos 35. Como 35 > 4, podemos dividir este número y escribir 35 ÷ 4 = 8 en la parte del cociente.
- Reste el resultado 4 × 8 = 32 de 35. Esto dará 3, y como es menor que 4, quedará como resto.
- 3 se conoce como resto y 108 como cociente.
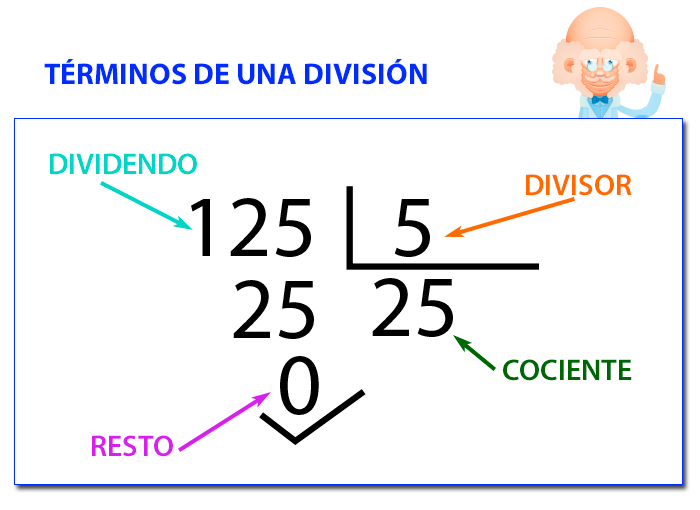
Partes de una división
- Dividendo: el dividendo es el número que se dividirá por el divisor.
- Divisor: el número por el cual se dividirá el dividendo se llama divisor.
- Cociente: la resultante de la división se llama cociente.
- Resto: el número que queda después de la división se llama resto.
División de 1 cifra
Suponga que desea encontrar 860 ÷ 5. Comience escribiendo el problema de esta manera:

La división se mueve de izquierda a derecha. En este caso, comience con el número en la columna de las centenas (8). Lo primero que debe hacer es preguntar cuántas veces 5 entra en 8, es decir, ¿cuánto es 8 ÷ 5? La respuesta es 1 (con un poco de sobra), así que escriba 1 en la parte del cociente (debajo del divisor). Ahora multiplique 1 x 5 para obtener 5, coloque la respuesta directamente debajo del 8 y dibuje una línea debajo de él.
Reste 8 – 5 para obtener 3. (Nota: Después de restar, el resultado siempre debe ser más pequeño que el divisor. De lo contrario, debes escribir un número más alto en el lugar del cociente). Luego, baja el 6 para hacer el nuevo número 36:
Estos pasos son un ciclo completo y para completar el problema solo necesita repetirlos. Ahora pregúntese cuántas veces 5 entra en 36, es decir, ¿cuánto es 36 ÷ 5? La respuesta es 7 (con un poco de sobra). Escriba 7 en el sector del cociente y luego multiplique 7 x 5 para obtener 35; escriba la respuesta debajo de 36:
Ahora reste para obtener 36 – 35 = 1; baje el 0 junto al 1 para hacer el nuevo número 10:

Otro ciclo está completo, así que comience el próximo ciclo preguntando cuántas veces 5 entra en 10, es decir, 10 ÷ 5. La respuesta esta vez es 2. Escriba el 2 en el cociente y multiplique 2 x 5 = 10. Escriba esta respuesta debajo del 10. Ahora reste 10 – 10 = 0. Como no tiene más números para reducir, ha terminado, y aquí está la respuesta:
Cociente: 860 ÷ 5 = 172.
División de 2 cifras
Paso 1: Comience tomando del dividendo el mismo número de dígitos que tenga el divisor. Si el número tomado del dividendo es menor que el divisor, debe seleccionar el siguiente dígito del dividendo.
Paso 2: Divida el primer número del dividendo (o los dos primeros números si el paso anterior tomó otro dígito) por el primer dígito del divisor. Escriba el resultado de esta división en el espacio del cociente.
Paso 3: Multiplique el dígito del cociente por el divisor, escriba el resultado debajo del dividendo y réstelo. Si no puede, porque el dividendo es menor, tendrá que elegir un número menor en el cociente hasta que pueda restarlo.
Paso 4: Después de la resta, suelte el siguiente dígito del dividendo y repita desde el paso 2 hasta que no queden más números en el dividendo. Ese es el concepto, pero lo analizaremos con un ejemplo.
Vamos a resolver la siguiente división de dos dígitos:

Tome los primeros dígitos del dividendo: en este caso 57. Pero como 57 es menor que 73, debe tomar un dígito más: 573. Para dividir 573 entre 73, tomamos los dos primeros dígitos del dividendo: 57 y los dividimos por el primer dígito del divisor:
57 ÷ 7 = 8
Escriba el 8 en el cociente y multiplícalo por el divisor:
8 x 73 = 584
Pero 584 es más grande que 573; por lo tanto, 8 «no encaja». Tienes que elegir el número anterior y volver a multiplicar:
7 x 73 = 511
511 es menor que el dividendo; por lo tanto, 7 «encaja». Escriba 511 debajo de los dígitos del dividendo y luego divida y reste:

Suelte el siguiente dígito del dividendo, que es 8. Ahora, debe dividir 628 entre 73. Para ello, repita los pasos anteriores. Divida los dos primeros dígitos del dividendo por el primer dígito del divisor y escriba en el espacio del cociente:
62 ÷ 7 = 8
Multiplique ese dígito por el divisor:
8 x 73 = 584
584 es menos de 628; por lo tanto, puede restar:
628 – 584 = 44

El resultado de esta división es 78 y el resto de 44.
Criterios de divisibilidad
Criterio de divisibilidad de 1
Todo número es divisible por 1, ya que la regla de divisibilidad para 1 no tiene ninguna condición. Cualquier número dividido por 1 dará el número en sí, independientemente de cuán grande sea. Por ejemplo, 3 es divisible por 1 y 3000 también es completamente divisible por 1.
Criterio de divisibilidad de 2
Si un número es par, siempre es completamente divisible por 2. Ejemplo: 508 es un número par y es divisible por 2, pero 509 no es un número par, por lo tanto, no es divisible por 2. El procedimiento para verificar si 508 es divisible por 2 o no es el siguiente:
- Considere el número 508
- Solo tome el último dígito 8 y divídalo por 2
- Si el último dígito 8 es divisible por 2, entonces el número 508 también es divisible por 2.
Criterio de divisibilidad de 3
La regla de divisibilidad para 3 establece que un número es completamente divisible por 3 si la suma de sus dígitos es divisible por 3. Considere un número, 308. Para verificar si 308 es divisible por 3 o no, tome la suma de los dígitos (es decir, 3 + 0 + 8 = 11). Ahora compruebe si la suma es divisible por 3 o no. Si la suma es un múltiplo de 3, entonces el número original también es divisible por 3. Aquí, dado que 11 no es divisible por 3, 308 tampoco es divisible por 3. De manera similar, 516 es divisible por 3 completamente como la suma de sus dígitos, es decir, 5 + 1 + 6 = 12, es un múltiplo de 3.
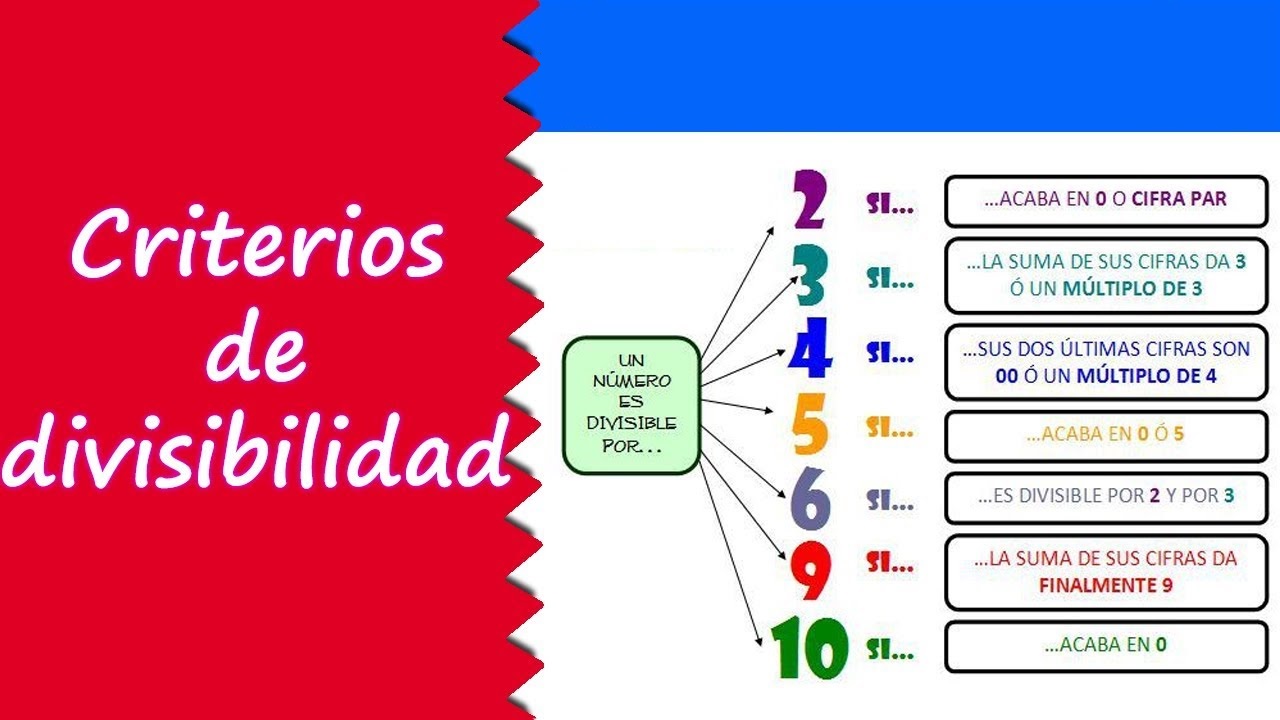
Criterio de divisibilidad de 4
Si los dos últimos dígitos de un número son divisibles por 4, entonces ese número es un múltiplo de 4 y es completamente divisible por 4. Ejemplo: Tome el número 2308. Considere los dos últimos dígitos, es decir, 08. Como 08 es divisible por 4, el número original 2308 también es divisible por 4.
Criterio de divisibilidad de 5
Los números, que terminan con dígitos 0 o 5, siempre son divisibles por 5. Ejemplo: 10, 10000, 10000005, 595, 396524850, etc.
Criterio de divisibilidad de 6
Los números que son divisibles por 2 y 3 son divisibles por 6. Es decir, si el último dígito del número dado es par y la suma de sus dígitos es un múltiplo de 3, entonces el número dado también es un múltiplo de 6. Ejemplo: 630, el número es divisible por 2 ya que el último dígito es 0. La suma de dígitos es 6 + 3 + 0 = 9, que también es divisible por 3. Por tanto, 630 es divisible por 6.
Criterio de divisibilidad de 7
La regla de divisibilidad por 7 es un poco complicada, lo que se puede entender mediante los pasos que se indican a continuación:
Ejemplo: ¿1073 es divisible entre 7?
- De la regla indicada, elimine 3 del número y duplíquelo, que se convierte en 6.
- El número restante se convierte en 107, por lo que 107-6 = 101.
- Repitiendo el proceso una vez más, tenemos 1 x 2 = 2.
- Número restante 10-2 = 8.
- Como 8 no es divisible entre 7, el número 1073 no es divisible por 7.
Criterio de divisibilidad de 8
Si los últimos tres dígitos de un número son divisibles por 8, entonces el número es completamente divisible por 8. Ejemplo: Tome el número 24344. Considere los dos últimos dígitos, es decir, 344. Como 344 es divisible por 8, el número original 24344 también es divisible por 8.

Criterio de divisibilidad de 9
La regla de divisibilidad por 9 es similar a la regla de divisibilidad de 3. Es decir, si la suma de dígitos del número es divisible por 9, entonces el número en sí es divisible por 9. Ejemplo: considere 78532, ya que la suma de sus dígitos (7 + 8 + 5 + 3 + 2) es 25, que no es divisible por 9, por lo tanto 78532 no es divisible por 9.
Criterio de divisibilidad de 10
La regla de divisibilidad para 10 establece que cualquier número cuyo último dígito sea 0 es divisible por 10. Ejemplo: 10, 20, 30, 1000, 5000, 60000, etc.
Criterio de divisibilidad de 11
Si la diferencia de la suma de dígitos alternativos de un número es divisible por 11, entonces ese número es completamente divisible por 11. Para verificar si un número como 2143 es divisible por 11, a continuación se muestra el siguiente procedimiento.
- Agrupe los dígitos alternativos, es decir, los dígitos que se encuentran en lugares impares y los dígitos en lugares pares. Aquí 24 y 13 son dos grupos.
- Tome la suma de los dígitos de cada grupo, es decir, 2 + 4 = 6 y 1 + 3 = 4
- Ahora encuentre la diferencia de las sumas; 6-4 = 2
- Si la diferencia es divisible por 11, entonces el número original también es divisible por 11. Aquí 2 es la diferencia que no es divisible por 11.
- Por tanto, 2143 no es divisible por 11.
Existen algunas condiciones más para probar la divisibilidad de un número por 11. Se explican aquí con la ayuda de ejemplos:
Si el número de dígitos de un número es par, sume el primer dígito y reste el último dígito del resto del número.
- Ejemplo: 3784
- Número de dígitos = 4
- Ahora, 78 + 3-4 = 77 = 7 × 11
- Por lo tanto, 3784 es divisible por 11.
Si el número de dígitos de un número es impar, reste el primer y último dígito del resto del número.
- Ejemplo: 82907
- Número de dígitos = 5
- Ahora, 290 – 8 – 7 = 275 × 11
- Por tanto, 82907 es divisible por 11.
Forme los grupos de dos dígitos desde el dígito del extremo derecho al extremo izquierdo del número y agregue los grupos resultantes. Si la suma es múltiplo de 11, entonces el número es divisible por 11.
- Ejemplo: 3774: = 37 + 74 = 111: = 1 + 11 = 12
- 3774 no es divisible por 11.
- 253: = 2 + 53 = 55 = 5 × 11
- 253 es divisible por 11.
Reste el último dígito del número del resto del número. Si el valor resultante es un múltiplo de 11, entonces el número original será divisible por 11.
- Ejemplo: 9647
- 9647: = 964 – 7 = 957
- 957: = 95 – 7 = 88 = 8 × 11
- Por lo tanto, 9647 es divisible por 11.
Criterio de divisibilidad de 12
Si el número es divisible por 3 y 4, entonces el número es exactamente divisible por 12.
- Ejemplo: 5864
- Suma de los dígitos = 5 + 8 + 6 + 4 = 23 (no múltiplo de 3)
- Últimos dos dígitos = 64 (divisible por 4)
- El número dado 5846 es divisible por 4 pero no por 3; por tanto, no es divisible por 12.
Criterio de divisibilidad de 13
Para cualquier número dado, para comprobar si es divisible entre 13, tenemos que sumar cuatro veces el último dígito del número al número restante y repetir el proceso hasta obtener un número de dos dígitos. Ahora compruebe si ese número de dos dígitos es divisible por 13 o no. Si es divisible, entonces el número dado es divisible por 13.
Por ejemplo: 2795 → 279 + (5 x 4)
→ 279 + (20)
→ 299
→ 29 + (9 x 4)
→ 29 + 36
→ 65
El número 65 es divisible por 13, 13 x 5 = 65.