La división a menudo se considera la más difícil de las cuatro funciones aritméticas principales. En esta página les explicaremos cómo realizar cálculos de división y, una vez que comprendamos bien el método y las reglas, podemos usar una calculadora para realizar cálculos más complicados sin cometer errores.

¿Qué son las divisiones?
La división de números enteros es la operación opuesta a la multiplicación de números enteros. Es cómo se intenta determinar cuántas veces un número está contenido en otro. Sabemos que dividir 20 entre 5 significa encontrar un número entero que, cuando lo multiplicamos por 5, nos da 20. Ese número entero es 4.
- Por lo tanto, escribimos 20 ÷ 5 = 4 o 20/5 = 4.
De manera similar, dividir 36 entre −9 significa encontrar un número entero que, cuando se multiplica por −9, da 36. Dicho número entero es −4.
- Por lo tanto, escribimos 36 ÷ (–9) = – 4 o, 36 / –9 = –4
Dividir (–35) entre (–7) significa qué número entero debe multiplicarse por (–7) para obtener (–35). Tal número entero es 5.
- Por lo tanto, (–35) ÷ (–7) = 5 o –35 / –7 = 5
Partes de las divisiones
Las partes de una división son las siguientes:
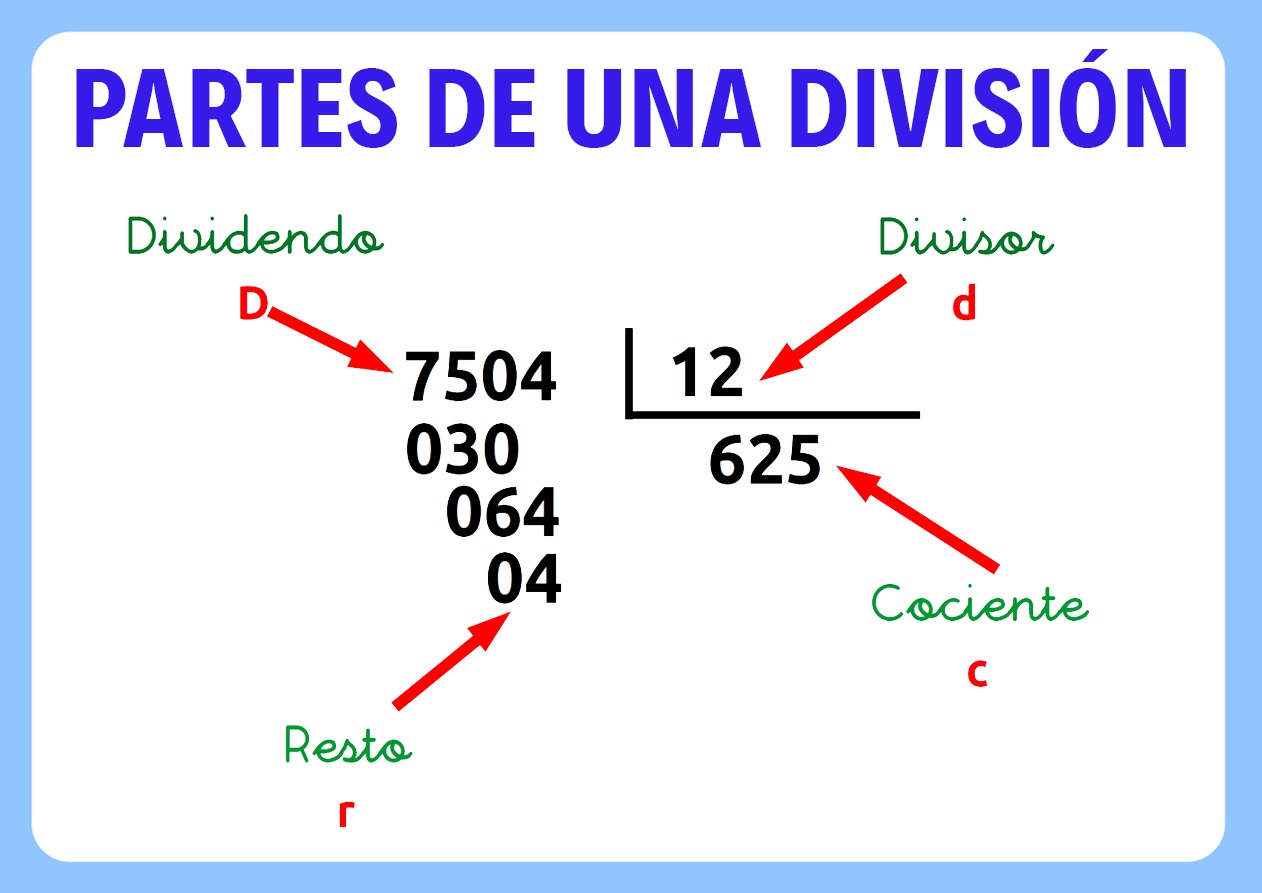
- Divisor: Es el número de partes en las que se va a dividir un número.
- Cociente: Es el resultado de la división. Más específicamente, es el tamaño de cada parte del número que se dividió por el divisor.
- Dividendo: Es el número a dividir.
- Resto: Es el resto que queda al hacer una división a mano antes de llegar a los decimales. Cuando una división tiene resto cero es porque ya no se puede dividir, a esto se le llama divisiones exactas. Pero cuando no tiene resto cero es porque las divisiones pueden continuar, estas se llaman divisiones enteras.
Propiedades de las divisiones
Las propiedades de la división se dan a continuación:
Propiedad 1: Si a y b (donde b no es igual a cero) son números enteros, entonces a ÷ b (expresado como a / b) no es necesariamente el número entero. En otras palabras, los números enteros no están cerrados para la división.
Verificación: sabemos que dividir un número entero a por un número entero b distinto de cero significa hallar un número entero c tal que a = bc. Considere la división de 14 entre 3. Encontramos que no hay un número entero que, cuando lo multiplicamos por 3, nos da 14. Entonces, 14 ÷ 3 no es un número entero. Del mismo modo, 12,5,9,4,37,6, etc., no son números enteros.
Propiedad 2: Si a es cualquier número entero, entonces a ÷ 1 = a. Esto significa que cualquier número real dividido por el número 1 da el cociente como el número mismo.
Verificación: sabemos que,
- 1 × 5 = 5 ∴ 5 ÷ 1 = 5
- 21 × 1 = 21 ∴ 21 ÷ 1 = 21
- 0 × 1 = 0 ∴ 0 ÷ 1 = 0
- 1 × 1 = 1 ∴ 1 ÷ 1 = 1 y así sucesivamente.
Propiedad 3: Si a es cualquier número entero distinto de cero, entonces a ÷ a = 1. De esta manera, también puede decir que cualquier número entero (que no sea cero) dividido por sí mismo da 1 como cociente.
Verificación: sabemos que,
- 12 = 12 × 1 ∴ 12 ÷ 12 = 1
- 7 = 7 × 1 ∴ 7 ÷ 7 = 1
- 6 = 6 × 1 ∴ 6 ÷ 6 = 1
- 1 = 1 × 1 ∴ 1 ÷ 1 = 1 y así sucesivamente.

Propiedad 4: Cuando cero se divide por cualquier número entero (que no sea cero), se obtiene el cociente como el número cero. En otras palabras, si a es un número entero distinto de cero, entonces 0 ÷ a = 0
Verificación: tenemos,
- 0 × 5 = 0 ∴ 0 ÷ 5 = 0
- 0 × 9 = 0 ∴ 0 ÷ 9 = 0
- 0 × 1 = 0 ∴ 0 ÷ 1 = 0 y así sucesivamente.
Observación: Para dividir 6 entre 0, debemos encontrar un número entero que, al multiplicarlo por 0, nos da 6. No se puede obtener tal número; decimos, por tanto, que la división entre 0 no está definida.
Propiedad 5: Sean a, b y c números enteros y b ≠ 0, c ≠ 0. Si a ÷ b = c, entonces b × c = a.
Verificación: tenemos,
- 12 ÷ 4 = 3 ∴ 3 × 4 = 12
- 42 ÷ 7 = 6 ∴ 7 × 6 = 42 y así sucesivamente. b × c = a.
Propiedad 6: Sean a, b y c los números enteros y b ≠ 0, c ≠ 0. Si b × c = a, entonces a ÷ c = b y a ÷ b = c
Verificación: tenemos,
- 12 = 3 × 4 ∴ 12 ÷ 3 = 4 y 12 ÷ 4 = 3
- 4 × 9 = 36 ∴ 36 ÷ 4 = 9 y 36 ÷ 9 = 4
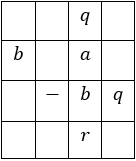
Propiedad 7: (Algoritmo de división) Si un número entero a se divide por un número entero b distinto de cero, entonces existen números enteros qyr tales que a = bq + r, donde r = 0 o r <b. Esto se puede expresar como:
Propiedades de la división en enteros
Hay algunas de las propiedades de una división de números enteros que se dan a continuación:
- Si a y b son números enteros, entonces a ÷ b no es necesariamente un número entero. Ejemplo: 14 ÷ 2 = 7. Aquí, el cociente es un número entero. Pero, en 15 ÷ 4, observamos que el cociente no es un número entero. Aquí, el resultado es 15/4 = 3 3/4. el cociente es 3; el resto es 3
- Si a es un número entero diferente de 0, entonces a ÷ a = 1.
- Para cada entero a, tenemos a ÷ 1 = a.
- Si a es un número entero distinto de cero, entonces 0 ÷ a = 0
- Si a es un número entero, entonces a ÷ 0 no es significativo.
- Si a, b, c son números enteros, entonces a> b ⇒ a ÷ c> b ÷ c, si c es positivo. a> b ⇒ a ÷ c <b ÷ c, si c es negativo.
¿Cómo dividir?
Realizar la división requiere la construcción de un cuadro. El divisor está separado del dividendo por un paréntesis derecho〈)〉 o una barra vertical〈|〉y el dividendo está separado del cociente por un vinculum (una barra superior). Ahora, sigamos los pasos de la división que se dan a continuación para comprender el proceso.
- Paso 1: Tome el primer dígito del dividendo de la izquierda. Compruebe si este dígito es mayor o igual que el divisor.
- Paso 2: Luego divídalo por el divisor y escriba la respuesta en la parte superior como el cociente.
- Paso 3: Reste el resultado del dígito y escriba la diferencia a continuación.
- Paso 4: Baje el siguiente dígito del dividendo (si está presente).
- Paso 5: Repita el mismo proceso.
Echemos un vistazo a los ejemplos que se dan a continuación para comprender mejor el concepto.
Divisiones de 1 cifra
Dividiendo un número de 2 dígitos por un número de 1 dígito
Siga los pasos a continuación para dividir un número de 2 dígitos por un número de 1 dígito. Utilizaremos como ejemplo la siguiente fórmula: 92 ÷ 4.
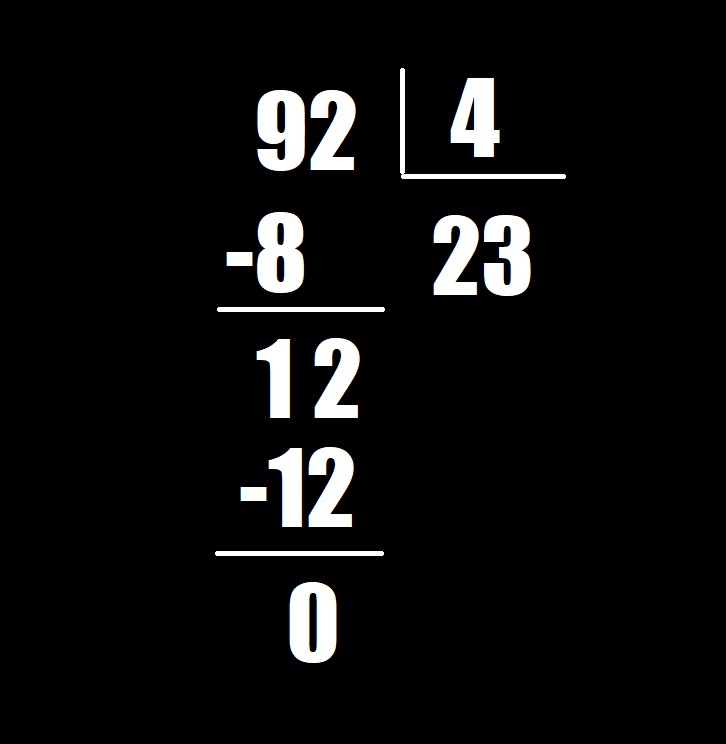
Para comenzar, sitúese en el dígito en el lugar de las decenas y calcule cuántas veces 4 entra en 9. Entra 2 veces, por lo que debe escribir el 2 encima del 9. Multiplique 4 × 2 = 8 y escriba el resultado debajo del 9. Reste 9–8 = 1 y le dará como resto 1.
Luego, baje el 2 del lugar de las unidades para crear el número 12 y calcule cuántas veces entra el 4 allí. Entra 3 veces, por lo que debes escribirlo encima del 2. Multiplique 4 × 3 = 12 y escriba el resultado debajo del 12. Reste 12-12 = 0 y le dará como resultado 0. Entonces, 92 ÷ 4 = 23!
Dividiendo un número de 3 dígitos por un número de 1 dígito
Siga los pasos a continuación para dividir un número de 3 dígitos por un número de 1 dígito. Probaremos con la fórmula 769 ÷ 3.
Para comenzar, nos situaremos en el dígito que se encuentra en el lugar de las centenas. Calcule cuántas veces 3 entra en 7, lo que nos dará como resultado 2 veces. Escriba el 2 encima del 7 y multiplique 3 × 2 = 6. Escriba el 6 debajo del 7 y reste 7–6 = 1. Le darás como resultado 1.

Luego, baja el 6 del lugar de las decenas para formar el número 16 y calcula cuántas veces entra el 3 allí. Nos darás como resultado que entra 5 veces. Escriba el 5 encima del 6 y multiplique 3 × 5 = 15. Escriba el 15 debajo del 16 reste 16-15 = 1. Le darás como resto 1.
Luego, baje el 9 del lugar de las unidades para formar el número 19. ¿Cuántas veces entra 3 en 19? Entra 6 veces. Escriba el 6 encima del 9 multiplique 3 × 6 = 18. Escriba el 18 debajo del 19 y reste 19-18 = 1. Le darás nuevamente como resto 1.
Allí se dará cuenta que no hay más dígitos para dividir, por lo que 1 es un resto. Eso significa que 3 no entra en 769 de manera uniforme. Entonces, 769 ÷ 3 = 256 Resto 1!
Dividiendo un número de 4 dígitos por un número de 1 dígito
Puede seguir los mismos pasos para dividir un número de 4 dígitos por un número de 1 dígito. Probaremos con 3042 ÷ 6.
Escribe el problema.
Comience con el dígito en el lugar de los miles. Allí nos daremos cuenta que 6 no entra en 3. Entonces, miramos los miles y los cientos juntos (que formarán el número 30). Calcule cuántas veces 6 entra en 30 (entra 5 veces). Escriba el 5 encima del 0 y multiplique 6 × 5 = 30. Luego, reste 30-30 = 0. Le dará como resultado 0.
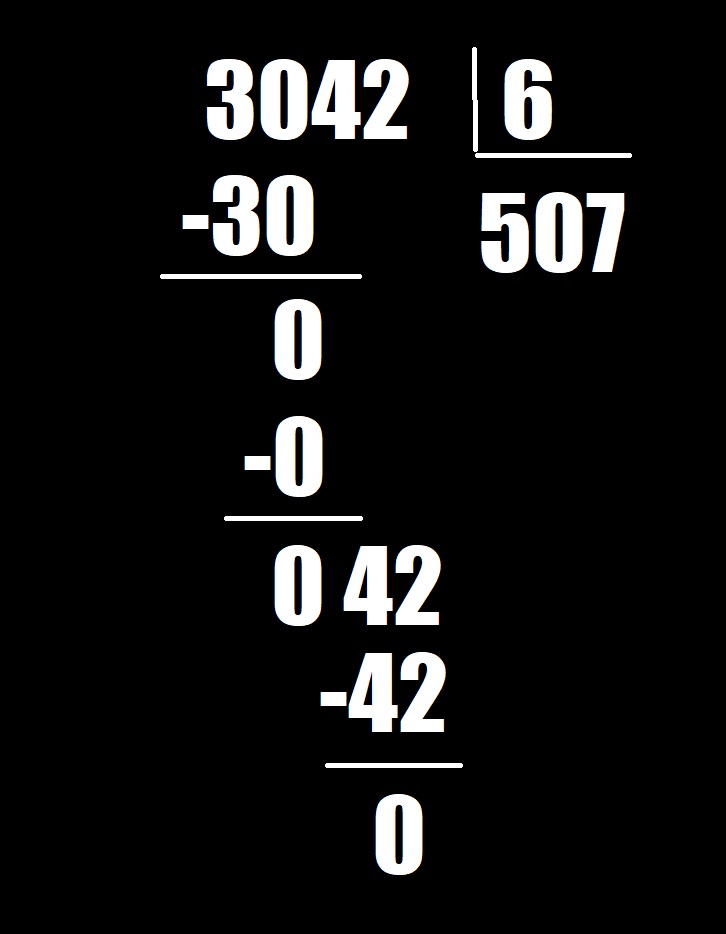
Luego, baje el 4 del lugar de las decenas para hacer el número 4. ¿Cuántas veces entra 6 en 4? Entra 0 veces. Escriba el 0 encima del 4 y multiplique 6 × 0 = 0. Luego, reste 4-0 y le dará como resultado 4.
Luego, baje el 2 del lugar de las unidades para formar el número 42. ¿Cuántas veces entra 6 en 42? Entra 7 veces, por lo que debe escribir el numero 7 encima del 2. Multiplica 6 × 7 = 42 y reste 42–42 = 0. Obtendremos como resultado 0, lo cual quiere decir que no habrá resto. Entonces, ¡3042 ÷ 6 = 507!
Divisiones de 2 cifras
Dividiendo un número de 3 dígitos por un número de 2 dígitos
Siga los pasos a continuación para dividir un número de 3 dígitos por un número de 2 dígitos. Pondremos a modo de ejemplo la siguiente formula: 649 ÷ 19.
Comience con el dígito en el lugar de las centenas. Dado que 19 no entra en 6, mire las centenas y las decenas juntas. Calcula cuántas veces 19 entra en 64. (Puede utilizar la siguiente estimación para ayudarse: el número 19 está cerca de 20 y 64 está cerca de 60. Dado que 60 ÷ 20 = 3, puede estimar que 19 entra en 64 aproximadamente 3 veces). Escriba el 3 encima del 4 y multiplique 19 × 3 = 57. Por ultimo, reste 64–57 y le dará como resto 7.
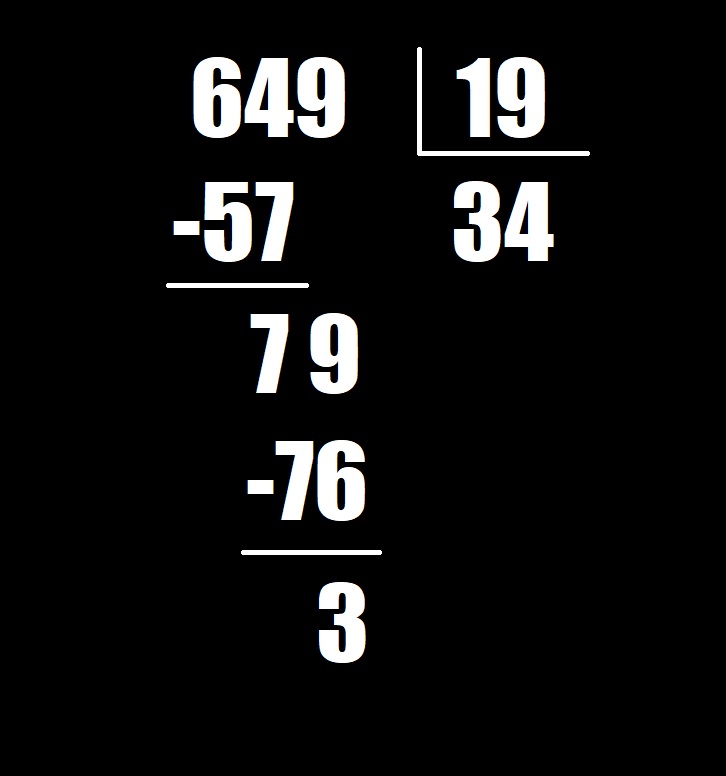
Luego, baje el 9 del lugar de las unidades para formar el número 79. ¿Cuántas veces entra 19 en 79? Puede utilizar la estimación de nuevo. El número 19 está cerca de 20 y 79 está cerca de 80. Dado que 80 ÷ 20 = 4, puede estimar que 19 entra en 79 aproximadamente 4 veces. Escriba el 4 encima del 9 multiplique 19 × 4 = 76. Luego, reste 79–76 y le dará como resto 3.
Una vez llegado a allí, nos daremos cuenta de que no hay más dígitos para dividir, por lo que 3 es un resto. Eso significa que 19 no puede entrar en 649 de manera uniforme. Entonces, 649 ÷ 19 = 34 resto 3!
Dividiendo un número de 4 dígitos por un número de 2 dígitos
Puede seguir los mismos pasos para dividir un número de 4 dígitos por un número de 2 dígitos. Probaremos con 8.526 ÷ 21.
Para comenzar, averigüe cuántas veces 21 entra en 85. Puede usar la estimación que mencionamos con anterioridad como ayuda. El número 21 está cerca de 20 y 85 está cerca de 80, por lo que 80 ÷ 20 = 4, puede estimar que 21 entra en 85 aproximadamente 4 veces.
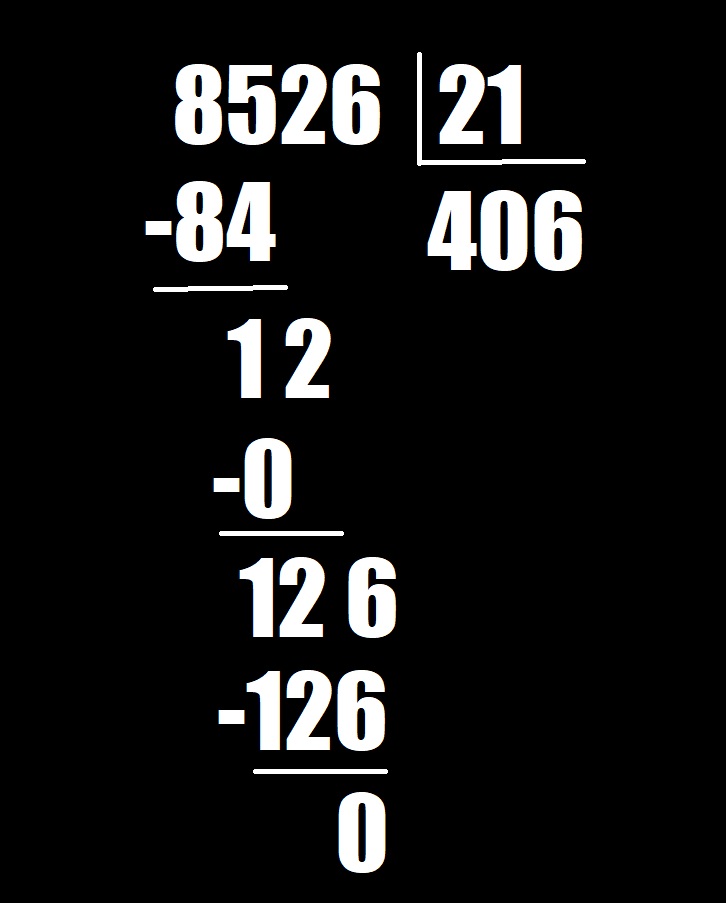
Escriba el 4 encima del 5 y multiplique 21 × 4 = A continuación, reste 85–84 y le dará como resto 1. Luego, baje el 2 del lugar de las decenas para firmar el número 12. ¿Cuántas veces entra 21 en 12? Entra 0 veces. Escriba el 0 encima del 2 y multiplique 21 × 0 = 0. A continuación reste 12-0 y le dará como resto nada más y nada menos que 12.
Luego, baje el 6 del lugar de las unidades para formar el número 126. ¿Cuántas veces entra 21 en 126? Puede utilizar la estimación de nuevo. El número 21 está cerca de 20 y 126 está cerca de 120. Dado que 120 ÷ 20 = 6, puedes estimar que 21 entra en 126 unas 6 veces. Escriba el 6 encima del 6 y multiplique 21 × 6 = 126. Luego, reste 126-126 y le dará como resultado 0, lo cual significa que no queda resto. Entonces, 8.526 ÷ 21 = 406!
Divisiones con decimales
En matemáticas, la división de decimales se puede observar en muchos conceptos como álgebra y geometría. Esta es bastante similar a la de fracciones, por lo que a continuación encontrarán un ejemplo que les dejará en claro cómo es que se hacen.
Ejemplo: Divida 0,2 entre 0,3.
Primero, convierta los decimales 0.2 y 0.3 en términos de la fracción.
- 0,2 = 2/10
- 0,3 = 3/10
Luego, arme la división y resuélvala:
- 0,2/0,3 = 2/10 ÷ 3/10= 2/10 × 10/3
- = 2/3
- = 0,666.
Por tanto, el resultado es 0,666
Divisiones con fracciones
Hay un atajo que puedes usar y que simplifica mucho la división de fracciones. A continuación les dejaremos los tres pasos principales:
- Voltee (o invierta) el divisor en un recíproco
- Cambie el signo de división a un símbolo de multiplicación y multiplique
- Simplifique su respuesta si es posible
Básicamente, lo que está haciendo al multiplicar fracciones es multiplicar la primera fracción por el recíproco de la segunda fracción. Pero a través de esta guía, profundizaremos en esto para simplificar la división de fracciones y ayudarlo a evitar las fracciones complejas.

Paso 1: Voltee el divisor en un recíproco
Un recíproco es un numero que multiplicas para obtener el valor de uno. Si desea convertir dos en uno mediante la multiplicación, debe multiplicarlo por 0.5. En forma de fracción, esto se ve así:
2/1 × 1/2 = 1
Para encontrar el recíproco de una fracción, simplemente voltee los números. El denominador se convierte en numerador y viceversa. Eche un vistazo a la ecuación de ejemplo nuevamente:
1/2 ÷ 1/6 =?
El primer paso para resolver el problema es convertir nuestro divisor, 1/6, en un recíproco.
1/6 → 6/1
Paso 2: Cambie el signo de división a un símbolo de multiplicación y multiplique
Dividir y multiplicar son opuestos entre sí. Cuando creas un recíproco de un número, también estás creando su opuesto. En un problema de división, cuando convierte el divisor en un recíproco, también necesita cambiar la ecuación de división a multiplicación. Ahora que ha encontrado el recíproco de su divisor, puede cambiar la ecuación de división a multiplicación.
1/2 ÷ 1/6 =? → 1/2 × 6/1 =?
- Multiplique los numeradores para obtener el nuevo numerador
- Multiplique los denominadores para obtener el nuevo denominador
- Simplifique la fracción final, si es posible
Para la ecuación de ejemplo, tienes dos problemas que resolver:
- 1 × 6 = 6
- 2 × 1 = 2
- 1/2 × 6/1 = 6/2
¡Ahora está listo para simplificar y obtener la respuesta final!
Paso 3: Simplifique su respuesta si es posible
Las fracciones simbolizan una parte de un todo. Esto significa que muchas fracciones representan el mismo valor, entonces, ¿por qué no hacer la fracción lo más simple posible? Por ejemplo, casi nunca dices cinco décimas o 5/10. En cambio, simplifica eso a la mitad o 1/2.
Para reducir una fracción a su forma más simple, divida el numerador y el denominador por su mayor factor común. El máximo factor común en 5/10 es cinco. Dividir ambos números por cinco te deja con 1/2.
En la pregunta del ejemplo, el máximo común divisor de 6/2 es dos. Esto convierte su solución de 6/2 a 3/1, que es lo mismo que decir tres. Por lo tanto:
1/2 ÷ 1/6 =? → 1/2 × 6/1 = 6/2 → 3/1 → 3
Crear un recíproco y multiplicar una ecuación en lugar de dividir le permite omitir varios pasos en una ecuación..
Ejercicios con divisiones para descargar
