Si estás buscando aprender qué es la multiplicación y cuáles son sus partes y propiedades, has llegado al lugar indicado. Aquí te enseñaremos a multiplicar por dos y tres cifras, y te dejaremos una gran cantidad de ejercicios para que puedas dominarlas fácil y rápidamente.

¿Qué es una multiplicación?
La multiplicación es una operación matemática de encontrar el resultado de dos o más números mediante la suma de los repetidos. Esta generalmente se denota con un signo de cruz (x). Sin embargo, también se utilizan otros símbolos como un asterisco (*), un punto (.) Y la frase «veces».
Partes de una multiplicación
Una multiplicación consta de dos partes, la expresión matemática y el producto. Una expresión matemática consta de factores y el operador o símbolo de la multiplicación. Por ejemplo, en una expresión matemática: 5 x 2 = 10, la porción «2 x 5» es la expresión matemática compuesta por 2 y 5 como factores y operadores. El producto, en este caso, es 10.
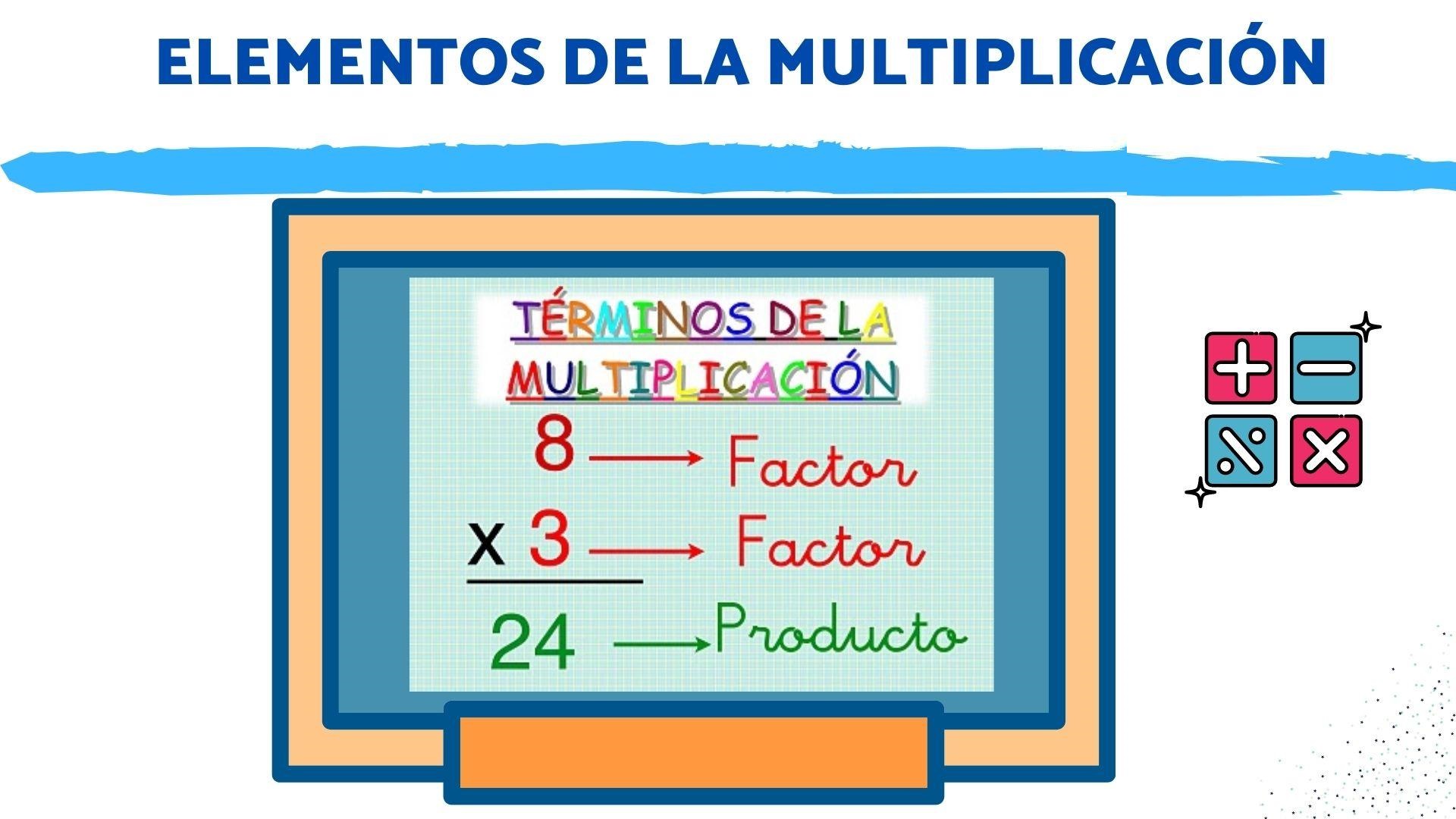
Podemos desglosar aún más los factores en multiplicando y multiplicador:
- Un multiplicando es un número multiplicado por otro número.
- Un multiplicador es un número con el que multiplicar.
- El producto es el resultado de multiplicar.
Propiedades de la multiplicación
El aprendizaje de las propiedades de la multiplicación ayuda a simplificar y resolver problemas matemáticos relacionados con la multiplicación.
Conmutativa
En la multiplicación, la propiedad conmutativa implica que la posición de los números no afecta la respuesta final (es decir, el orden de los factores no altera al producto). En general, para una oración de multiplicación: m x n = n x m. Por ejemplo, 4 x 5 es lo mismo que 5 x 4. Esta propiedad también se aplica cuando se multiplica un grupo grande de números. Por ejemplo, 4 x 3 x 2 = 2 x 3 x 4.
Asociativa
En la multiplicación, la propiedad asociativa establece que la agrupación de números no afecta la respuesta final cuando se multiplica una serie de números. Generalmente, las agrupaciones en cualquier expresión matemática se indican entre paréntesis o corchetes. Podemos resumir esta propiedad como: m x (n x p) = (m x n) x p. Por ejemplo, (2 x 4) x 6 = 2 x (4 x 6).

Identidad
Esta propiedad establece que la multiplicación de cualquier número con el número uno no cambia su valor. En otras palabras, esta propiedad se puede escribir como 1 x a = a. Por ejemplo, 1 x 8 = 8.
Distributiva
La propiedad distributiva para la multiplicación establece que una expresión que consiste en la suma o resta de valores multiplicados por un número es equivalente a la suma o diferencia de los números de expresión. En general, m x (n + p) = m x n + m x p, y m x (n – p) = m x n – m x p. Por ejemplo, 2 x (3 + 4) = 2 x 3 + 2 x 4.
Multiplicación de 2 cifras
La multiplicación de dos dígitos es simplemente una multiplicación de un solo dígito que se hace dos veces. Comienza de la misma manera multiplicando los números en el lugar de las unidades, y luego agrega una segunda ronda de multiplicación usando los números del lugar de las decenas. Después de aprender la fórmula básica, también hay algunos trucos que puede dominar para que este proceso se desarrolle lo más rápido posible.

1. Multiplique y lleva los resultados que son mayores que 9. Si multiplicas el número de lugar de las unidades y el resultado es mayor que 9, necesitarás llevar el valor adicional por encima del número superior. Recuerda escribir el valor extra sobre el lugar de las decenas. Por ejemplo, si estás multiplicando 96 por 8, cuando multiplicas el 6 por 8, obtendrás 48. En lugar de escribir 48 debajo de tu línea, escribe un 8 y lleva el 4.
2. Multiplique el lugar de las decenas y sume el valor registrado. Multiplique el lugar de la última unidad y el lugar de la parte superior de la decena como lo haría normalmente. Luego sume el valor que llevaste por encima del lugar de las decenas. Por ejemplo, para 96 x 8, multiplica 8 y 9 para obtener 72. Luego suma el 4 que llevaste para obtener 76. Esto te dará una respuesta final de 768.
3. Continúe multiplicando y transportando si es necesario. Si 1 de sus números tiene más de 2 dígitos, siga multiplicando y trasladando el número hasta que los haya trabajado todos.
Ejercicios de multiplicación x 2 cifras
Multiplicaremos: 63 × 24.
Primero, escriba el problema y alinee los números por valor posicional.
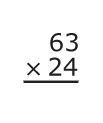
Luego, multiplique el número de arriba por el dígito de las unidades del número de abajo. En este ejemplo, multiplique 63 × 4.
3 × 4 = 12
Reagrupe 12 de la siguiente manera: 1 en las decenas y 2 en las unidades.

6 × 4 = 24
Sume el 1 de la decena que reagrupó.
24 + 1 = 25
Luego, multiplique el número superior por el dígito de las decenas del número inferior. En este ejemplo, multiplique 63 × 2. Debido a que el 2 representa decenas, los números comenzarán en la columna de las decenas. Coloque un 0 en la columna de las unidades.
3 × 2 = 6
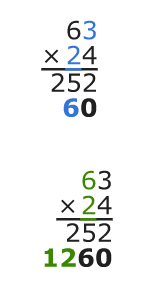
6 × 2 = 12
Por último, agregue los productos. Recuerde reagrupar si es necesario.

Entonces, 63 × 24 = 1,512!
Multiplicaremos: 63 x 14
(i) Primer método
63 x 14
= (60 + 3) × (10 + 4)
= (60 + 3) × 10 + (60 + 3) × 4
= (600 + 30) + (240 + 12)
= 630 + 252
= 882
o bien, 63 × 14 = (60 + 3) (10 + 4)
= (60 + 3) x 4 + (60 + 3) x l0
= (240 +12) + (600 + 30)
= 252 + 630
= 882
(ii) Segundo método
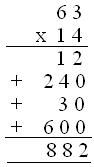
(a) 4 × 3 unidades = 12 unidades
(b) 4 × 6 decenas = 24 decenas = 240 unidades
(c) 1 decena × 3 unidades = 3 decenas = 30 unidades
(d) 1 decena = 10 × 6 decenas = 10 × 60 unidades = 600 unidades
(iii) Tercer método
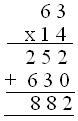
(a) 14 = (10 + 4)
(b) 63 × 4 = 252
(c) 63 × 10 = 630
(iv) Cuarto método
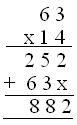
(a) 14 = 4 unidades + 1 decena
(b) 63 × 4 unidades = 252 unidades
(c) 63 × 1 decena = 63 decenas
(Generalmente se adopta el cuarto método)
Multiplicación de 3 cifras
La multiplicación de tres dígitos es simplemente una multiplicación de un solo dígito que se hace tres veces. Comienza de la misma manera multiplicando los números en el lugar de las unidades, luego agrega una segunda ronda de multiplicación usando los números del lugar de las decenas, y por ultimo termina con una tercer ronda de multiplicación utilizando los números en el lugar de la centenas.
1. Multiplique y lleva los resultados que son mayores que 9. Si multiplicas el número de lugar de las unidades y el resultado es mayor que 9, necesitarás llevar el valor adicional por encima del número superior. Recuerda escribir el valor extra sobre el lugar de las decenas. Por ejemplo, si estás multiplicando 196 por 8, cuando multiplicas el 6 por 8, obtendrás 48. En lugar de escribir 48 debajo de tu línea, escribe un 8 y lleva el 4.

2. Multiplique el lugar de las decenas y sume el valor registrado. Multiplique el lugar de la última unidad y el lugar de la parte superior de la decena como lo haría normalmente. Luego sume el valor que llevaste por encima del lugar de las decenas. Por ejemplo, para 196 x 8, multiplica 8 y 9 para obtener 72. Luego suma el 4 que llevaste para obtener 76. De esta forma deje el 6 y lleve el 7 por encima del lugar de la centena.
3. Multiplique el lugar de las centenas y sume el valor registrado. Multiplique el lugar de la última unidad y el lugar de la parte superior de la centena como lo haría normalmente. Luego sume el valor que llevaste por encima del lugar de las centenas. Por ejemplo, para 196 x 8, multiplique 8 y 1 para obtener 8. Luego suma el 7 que llevaste para obtener 15. Sume todo y obtendrá el resultado: 1568.
3. Continúe multiplicando y transportando si es necesario. Si 1 de sus números tiene más de 2 dígitos, siga multiplicando y trasladando el número hasta que los haya trabajado todos.
Ejercicios de multiplicación x 3 cifras
Hallar el producto de 36 × 137
(I) Primer método
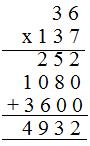
(a) 137 = 7 + 30 + 100
(b) 36 × 7 = 252
(c) 36 × 30 = 1080
(d) 36 × 100 = 3600
(ii) Segundo método
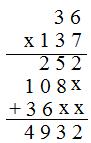
(a) 137 = 7 unidades + 3 decenas + 1 centena
(b) 36 × 7 unidades = 252 unidades
(c) 36 × 8 decenas = 108 decenas
(d) 36 × 1 cien = 36 centenas
Hallar el producto de 543 x 278
(i) Primer método
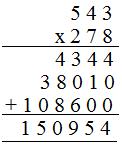
(a) 278 = 8 + 70 + 200
(b) 543 × 8 = 4344
(c) 543 × 70 = 38010
(d) 543 × 200 = 108600
Producto = 150954
(ii) Segundo método
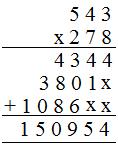
(a) 278 = 8 unidades + 7 T + 2 H
(b) 543 × 8 unidades = 4344 unidades
(c) 543 × 7 T = 3801 decenas
(d) 543 × 2 H = 1086 centenas
Producto = 150954
Hallar el producto de 827 × 107
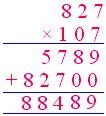
→ 100 + 7
Multiplicar por 7
Multiplicar por 100
Respuesta: 88489
Hallar el producto de 474 × 240
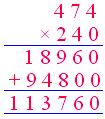
→ 200 + 40
Multiplicar por 40
Multiplicar por 200
Respuesta: 113760
Halla el producto de 528 x 378.
Paso I: Organiza los números verticalmente.
Paso II: Multiplica 528 por 8
528 × 8 = 4224.
Paso III: Multiplica 528 por 70
528 × 70 = 36960.
Paso IV: Multiplica 528 por 300
528 × 300 = 158400.
Paso V: Agregar: 4224, 36960 y 158400
4224 + 36960 + 158400 = 199584
Hallar el producto de 2437 x 324
(i) Primer método
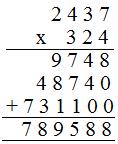
(a) 324 = 4 + 20 + 300
(b) 2437 × 4 = 9748
(c) 2437 × 20 = 48740
(d) 2437 × 300 = 731100
El producto = 789588
(ii) Segundo método
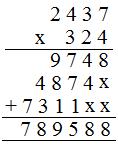
(a) 324 = 4 unidades + 2 decenas + 3 centenas
(b) 2437 × 4 unidades = 9748 unidades
(c) 2437 × 2 T = 4874 decenas
(d) 2437 × 3 H = 7311 centenas
El producto = 789588