Un triángulo es un polígono con tres aristas y tres vértices. Es una de las formas básicas en geometría. En la geometría euclidiana, cualquiera de los tres puntos, cuando no son colineales, determinan un triángulo único y, simultáneamente, un plano único (es decir, un espacio euclidiano bidimensional).

En otras palabras, solo hay un plano que contiene ese triángulo, y cada triángulo está contenido en algún plano. Si toda la geometría es solo el plano euclidiano, solo hay un plano y todos los triángulos están contenidos en él; sin embargo, en los espacios euclidianos de dimensión superior, esto ya no es cierto. Este artículo trata sobre los triángulos en la geometría euclidiana, y en particular, el plano euclidiano, excepto donde se indique lo contrario.
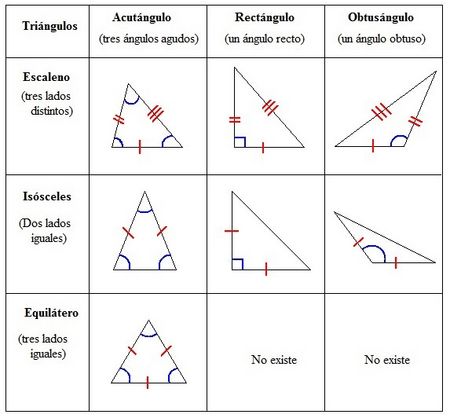
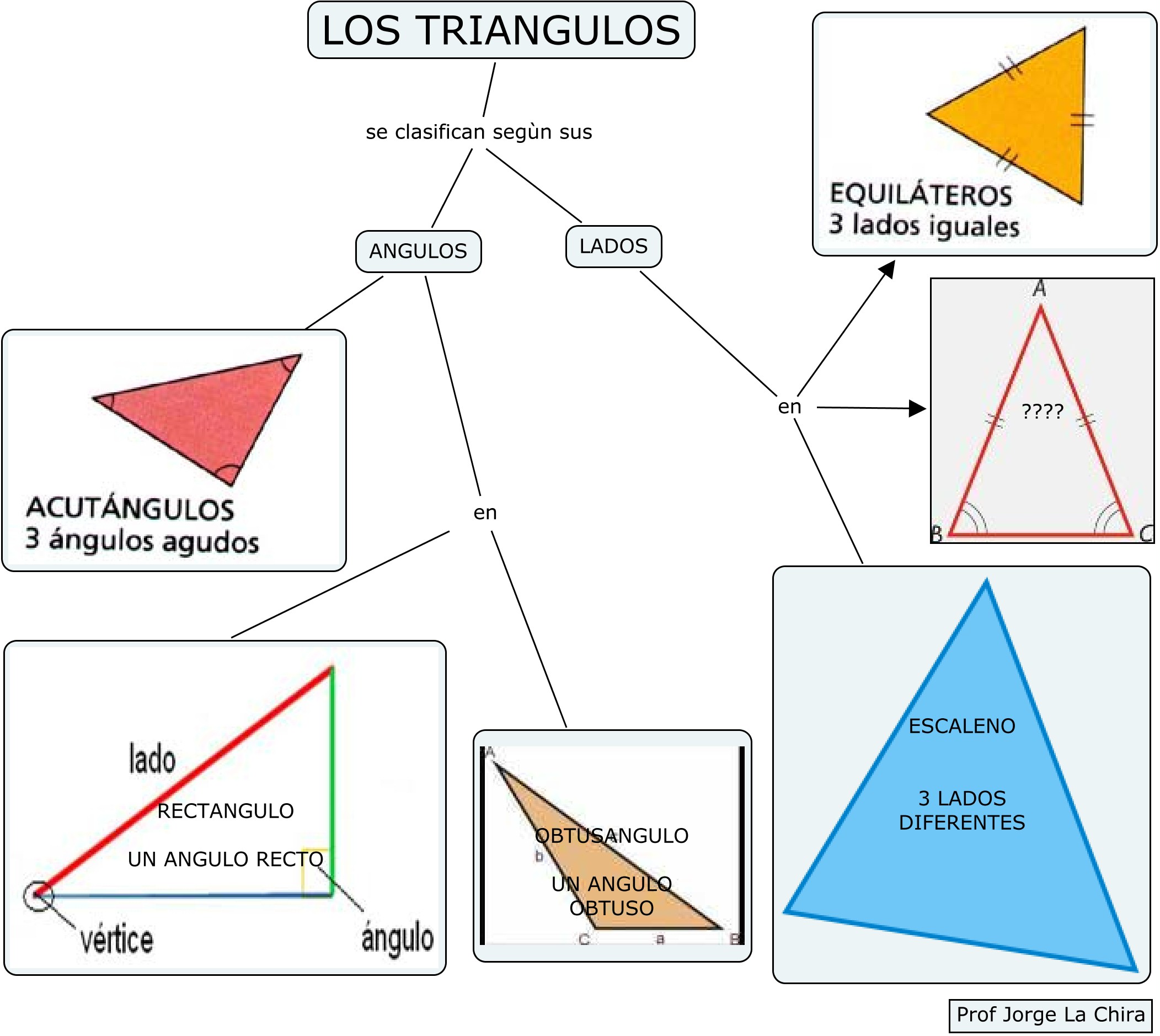
Los elementos básicos de cualquier triángulo son sus lados y ángulos. Los triángulos se clasifican en función de los tamaños relativos de sus elementos.
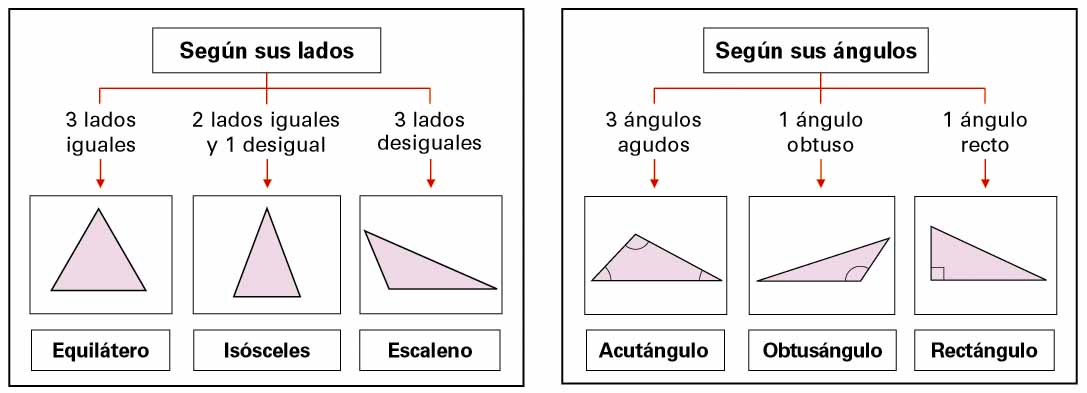
Respecto a sus lados, los triángulos pueden ser:
- Escaleno (todos los lados son diferentes)
- Isósceles (dos lados son iguales)
- Equilátero (los tres lados son iguales)
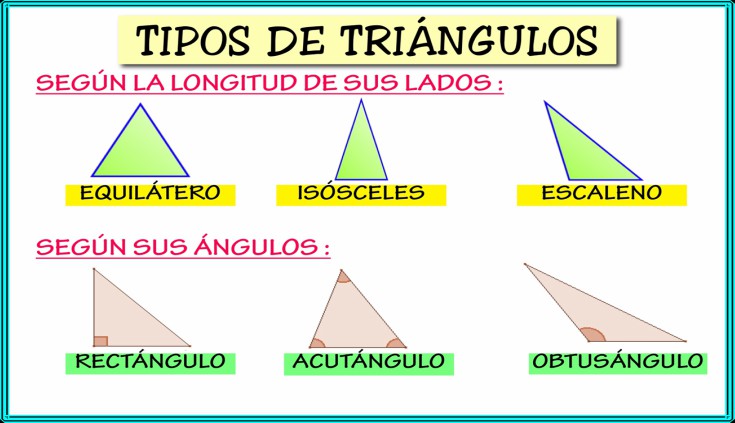
Y en cuanto a sus ángulos, los triángulos pueden ser
- Agudo (todos los ángulos son agudos)
- Derecha (un ángulo es correcto)
- Obtuso (un ángulo es obtuso)
- Equiangular (todos los ángulos son iguales)
Triángulos según lados
Un triángulo es escaleno si todos sus tres lados son diferentes (en cuyo caso, los tres ángulos también son diferentes). Si dos de sus lados son iguales, un triángulo se llama isósceles. Un triángulo con los tres lados iguales se llama equilátero. Las palabras de las matemáticas de S. Schwartzman explican la etimología (los orígenes) de las palabras. Los dos primeros son de origen griego (y afines); La palabra «equilátero» es de origen latino.

Triángulo Escaleno
El adjetivo escaleno viene de la raíz indoeuropea «a cortar». Los skalenos griegos originalmente querían decir «agitados, amarrados». Cuando se agita un trozo de tierra, la superficie se vuelve «desigual», que fue un significado posterior de skalenos.
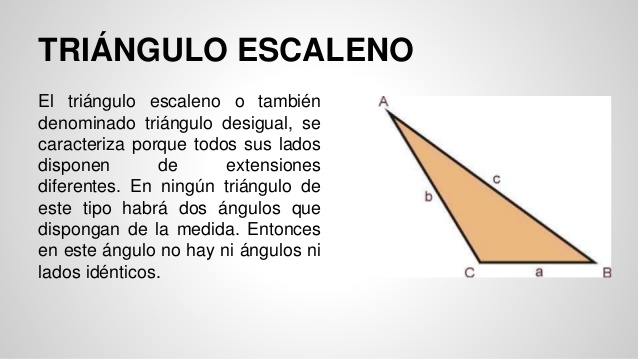
Un triángulo escaleno es desigual en el sentido de que los tres lados son de diferentes longitudes. Los músculos escalenos en cada lado del cuello de una persona reciben su nombre por su apariencia triangular. Un cono o cilindro escaleno es aquel cuyo eje no es perpendicular a su base; Los elementos opuestos forman ángulos «desiguales» con la base.
Triángulo isósceles
Isósceles (adjetivo): del griego isos «igual», de origen anterior desconocido, y skelos «pierna». La raíz (s) indoeuropea kel- «curvada, doblada» se encuentra en la escoliosis y el colon, tomados del griego.
En geometría, un triángulo isósceles o trapecio tiene dos patas iguales. Puede parecer extraño que la raíz signifique «doblada» aunque los lados de un triángulo o trapecio estén rectos, pero cada pierna está doblada en relación con las piernas adyacentes.
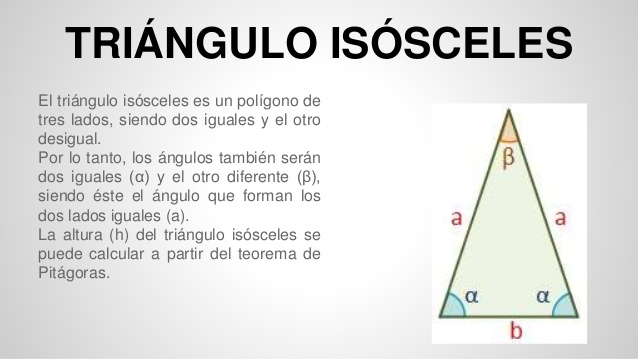
En geometría, un triángulo isósceles es un triángulo que tiene dos lados de igual longitud. A veces se especifica que tiene exactamente dos lados de igual longitud, y otras veces que tiene al menos dos lados de igual longitud, la última versión incluye así el triángulo equilátero como un caso especial.
Los ejemplos de triángulos isósceles incluyen el triángulo rectángulo isósceles, el triángulo dorado y las caras de las bipirámides y ciertos sólidos catalanes. El estudio matemático de los triángulos isósceles se remonta a las antiguas matemáticas egipcias y las matemáticas babilónicas. Los triángulos isósceles se han utilizado como decoración desde épocas anteriores y aparecen con frecuencia en la arquitectura y el diseño, por ejemplo, en los frontones y frontones de los edificios.
Los dos lados iguales se llaman patas y el tercer lado se llama la base del triángulo. Las otras dimensiones del triángulo, como su altura, área y perímetro, se pueden calcular mediante fórmulas simples a partir de las longitudes de las piernas y la base.
Cada triángulo isósceles tiene un eje de simetría a lo largo de la bisectriz perpendicular de su base. Los dos ángulos opuestos a las piernas son iguales y siempre son agudos, por lo que la clasificación del triángulo como aguda, derecha u obtusa depende solo del ángulo entre sus dos piernas.
Triángulo Equilatero
Equilátero (adjetivo): del latín æquus «par, nivel» y latus, raíz posterior, «lado», ambos de origen incierto. Los préstamos relacionados del latín son bilaterales y multilaterales. En geometría, triángulo equilátero es uno en el que todos los lados son iguales en longitud.
Un triángulo equilátero es simplemente un caso específico de un polígono regular, en este caso con 3 lados. Todos los hechos y propiedades descritos para los polígonos regulares se aplican a un triángulo equilátero.
Propiedades
- Los tres ángulos de un triángulo equilátero son siempre 60 °. En la figura anterior, los ángulos ∠ABC, ∠CAB y ∠ACB son siempre los mismos. Dado que los ángulos son iguales y los ángulos internos de cualquier triángulo siempre suman 180 °, cada uno es 60 °.
- El área de un triángulo equilátero se puede calcular de la manera habitual, pero en este caso especial de un triángulo equilátero, también viene dada por la fórmula:
- Área =
√ 3
4
s 2
donde S es la longitud de cualquier lado. Ver Área de un triángulo equilátero. - Con un triángulo equilátero, el radio del incírculo es exactamente la mitad del radio del circuncírculo.
Tipos de triángulo por ángulo
- En un triángulo equiangular, todos los ángulos son iguales, cada uno mide 60 grados. Un triángulo equiangular es un tipo de triángulo agudo, y siempre es equilátero.
- En un triángulo rectángulo, uno de los ángulos es un ángulo recto: un ángulo de 90 grados. Un triángulo rectángulo puede ser isósceles o escaleno.
- En un triángulo obtuso, un ángulo es mayor que un ángulo recto: tiene más de 90 grados. Un triángulo obtuso puede ser isósceles o escaleno.
- En un triángulo agudo, todos los ángulos son menores que los rectos, cada uno tiene menos de 90 grados. Un triángulo agudo puede ser equilátero, isósceles o escaleno.

Hechos básicos de los triángulos
Se supone que los triángulos son figuras planas bidimensionales, a menos que el contexto proporcione lo contrario, un triángulo se denomina 2-simplex (véase también Polytope). Euclides presentó los datos elementales sobre los triángulos en los libros 1 a 4 de sus Elementos, alrededor del 300 a.
- Las medidas de los ángulos interiores del triángulo siempre suman 180 grados (del mismo color para señalar que son iguales).
- La suma de las medidas de los ángulos interiores de un triángulo en el espacio euclidiano es siempre 180 grados.
- Este hecho es equivalente al postulado paralelo de Euclides. Esto permite determinar la medida del tercer ángulo de cualquier triángulo dada la medida de dos ángulos. Un ángulo exterior de un triángulo es un ángulo que es un par lineal (y por lo tanto complementario) a un ángulo interior.
- La medida de un ángulo exterior de un triángulo es igual a la suma de las medidas de los dos ángulos interiores que no están adyacentes a él; Este es el teorema del ángulo exterior. La suma de las medidas de los tres ángulos exteriores (uno para cada vértice) de cualquier triángulo es 360 grados.
- Se dice que dos triángulos son similares si cada ángulo de un triángulo tiene la misma medida que el ángulo correspondiente en el otro triángulo. Los lados correspondientes de triángulos similares tienen longitudes que están en la misma proporción, y esta propiedad también es suficiente para establecer la similitud.
- Si y solo si un par de ángulos internos de dos triángulos tienen la misma medida entre sí, y otro par también tiene la misma medida entre sí, los triángulos son similares.